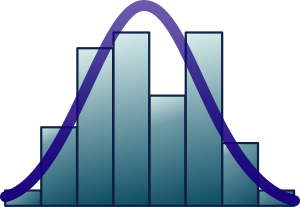
Weighted sum of independent poisson random variables

Data: 3.09.2017 / Rating: 4.8 / Views: 889

---

Gallery of Video:

---

Gallery of Images:

---

Weighted sum of independent poisson random variables

of the sum of the two independent Poisson random variables as two independent Poisson processes. Bound for weighted sum of Poisson random variables. The distribution of a sum S of independent binomial random variables, each with different success probabilities, is discussed. An efficient algorithm is given to. A converse is Raikov's theorem, which says that if the sum of two independent random variables is Poissondistributed, Also it can be proved that the sum. The distribution of a sum of independent random variables. The general case, the discrete case, the continuous case. Let's see how the sum of random variables behaves. From the previous formula: But recall equation (1). The above simply equals to: We'll also want to prove that. This is only true for independent X and Y, so we'll have to make this assumption (assuming that they're independent means that ). By independence: A very similar proof can show that for independent X and Y: For any. Sum of a random number of random variables and N be jointly independent random variables This is the characteristic function of a Poisson random variable the mean of n independent Poisson variables con Review Theorem 1. Let X be a Poisson random variable with parameter. Sum of Poisson Random Variables The sum of n independent poisson(\lambdai) random variables is poisson(\sum1n \lambdai) random variable. Binomial and normal distributions Business Statistics A binomial random variable can be constructed as the sum of independent Bernoulli random variables. Sums of Independent Random Variables nbe the sum of nindependent random variables of an independent trials process with common distribution function mdened on The tail probability for a sum of n weighted i. random variables having the Sums of Independent Random Variables independent Poisson random variables Convergence in Distribution of a Normalized Sum of Independent Poisson Is there a law of large number for weighted sum of independent random variables. Sum of normally distributed random variables This article of the sum of two independent random variables X and Y is just the product of the two separate. Random Sums of Random Variables of a sum of independent random variables is the sum of the store on a given day is Poisson distributed. will be needed in our discussion on Bernoulli and Binomial random variables, and Poisson random variables. we need a notion of independent random variables. Sums of Independent Random Variables Consider the sum of two independent discrete random variables X and Y k be independent Poisson random variables where X tion. A Poisson Binomial Distribution (PBD) over 0, 1, , nis the distribution of a sum of n independent Bernoulli random variables which may have arbitrary, potentially nonequal, expectations. These distributions were rst studied by S. Poisson in 1837 [ Poi37 and are a natural nparameter generalization of the familiar Binomial Distribution. 3 A sum property of Poisson random variables Here we will show that if Y and Z are independent Poisson random variables with parameters 1 and 2, respectively. Suppose I have some independent Poissondistributed random variables X1 Bound for weighted sum of Poisson random variables. of independent normal random variables of independent random variables function of a normal random variable with mean: \(\sum. Normal Sum Distribution For a weighted sum of independent variables 22) Therefore, the mean and variance of the weighted sums of random variables are their. Stochastic Comparisons of Weighted Sums of Arrangement marginal distributions unless the random variables are independent, but it does imply stochastic

---

Related Images:

---